I consider myself very much in line with your stereotypical utilitarian-EA-rationalist-analytic philosophy type. I am a longtermist, a fanatic, I think animal and insect suffering is a huge issue, that consequentialism is the correct moral theory, that the analytic method is deeply valuable and our best tool for getting to foundational truths, and that morality is significantly more demanding than any of us realize.
With all that said, however, there is a philosophical issue on which I break rank with your stereotypical rationalist. I am not an additive aggregationist. I endorse a position that I have termed ‘bounded aggregation’. Let me explain.
All (or, the vast, vast majority of) moral theories have something called a theory of the good, or a theory of value. These are theories of what things are valuable or good. For instance, many theories of the good claim that well-being is something with intrinsic value. If a world contains a creature that is well off, the world is better off for having such a creature.1 Similarly, many theories of value claim that suffering is intrinsically disvaluable.
Now, there are lots of fights about what the right theory of value is. We can set all of that aside. What is important to see is that, in addition to your theory of value, you need what I call a theory of aggregation. A theory of aggregation is a theory that tells you how to aggregate value.
An informal example will be helpful. Suppose you have a theory of value on which pain is intrinsically disvaluable. Okay. Now, suppose there is a world with 1 headache. Call this world H1. H1 has some disvalue. Let’s say that the disvalue of the headache is such that the world’s total value is -1. Great. Now imagine another world, just like H1, except that here there are two people experiencing mild headaches. Let’s call this world H2. Question: how much disvalue is in H2? You might want to say: well, we said H1 has total value -1. So, it must be that H2 has total value -2.
That answer assumes a certain theory of value aggregation. In particular, it assumes an additive theory of aggregation. An additive theory of aggregation claims (again, this is all informal — a formal exposition will be coming) that if the value of x is n, and the value of y is m, the total value in a world with x and y is n + m.
So, a theory of aggregation is a theory that tells us how to determine the total value in a world, given the individual values of each component part of a world. An additive theory of aggregation is one that says the total value in a world is merely the sum of the values of the component parts of a world. Reasonable enough, right? Well, that’s what they want you to think…
Here is a reason to think the additive theory is false.
Compare H1 and H2 to another world, where there is 1 person experiencing torturous suffering. This person is screaming as he is slowly suffocated to death with his skin being burned off and his organs pulled apart (a fate similar to what billions of screaming chickens experience because we value our own gustatory pleasures). Let’s call this world T1. T1 is also disvaluable — very disvaluable. Let’s say the suffering here is so intense that T1 has a total disvalue of -1000. Okay. But this has an odd implication: if there is a world with 1001 people each experiencing a mild headache — call it H1001 — the additive theory entails that H1001 is more disvaluable than T1. That is to say, you should prefer that the world be such that 1 person experiences mind-numbing torture than for 1001 people to experience barely-noticeable headaches. But that’s absurd! If it were up to me — if I could choose which world were the case — I would let millions of people experience barely-noticeable headaches before I ever let it be that a single person experience this kind of torture. But then it can’t be that 1001 headaches “add up” to be more disvaluable than horrific torture.
You might say that this simply means our numbers were off. But the problem, to me, is that no set of numbers will ever be satisfactory. For any n, Hn is preferable to T1. But then the additive theory has to be false: for this is just to say that no amount of headaches could ever “add up” to be more disvaluable than horrific torture.
You might try to say that all this shows is that torture is infinitely disvaluable, not that we should reject the additive theory of aggregation. But I think it is rather clear that torture is not infinitely disvaluable: two instances of torture are surely more disvaluable than a single instance of torture, and torture can be traded off with other less-bad things (i.e., a world with 20 instances of slightly-less-bad torture is more disvaluable than T1, even though both are more disvaluable than Hn, for any n).2
Finally, you might object by saying that all this shows is that consequentialism is false. This just goes to show that sometimes you shouldn’t care about aggregate value! Sadly, this is deeply mistaken. The problem here has nothing to do with whether you are a consequentialist or deontologist. The intuition I am appealing to is that, no matter what n is, T1 has more disvalue than Hn! That is to say, the total disvalue involved in torture is more than the total disvalue involved in n headaches — it is preferable that n headaches obtain than that a single instance of torture obtain. This is an intuition about total value and the preferability of certain states of affairs over others.
Okay, if additive aggregation is false, what should we endorse? I advocate for what I call bounded aggregation. Bounded aggregation claims that, at least for some kinds of harms, there is a bound to how much disvalue they can contribute. Here’s one way such a theory could go: a single headache has a disvalue of -1. However, the aggregate disvalue of 2 headaches is not -2. Instead, it is -1.5. And the aggregate disvalue of 3 headaches is -1.75. I.e., as there are more and more headaches, the total value of a world with these headaches corresponds to a geometric series with a bound of -2: -1 + -0.5 + -0.25 + …
This secures the result that, no matter how many headaches you have in the world, the total disvalue in the world will never be more than -1000. There is a limit to just how bad n headaches could ever make the world. And that’s pretty intuitive! This is one example of a non-additive theory of value aggregation.
Alright, all of that was rather informal and incomplete. And there are very many possible objections to consider. Here’s the plan for the rest of this article: first, I will formalize things for the sake of clarity, and then address some objections to bounded aggregation. However, I hope that the main takeaway from this article is that value aggregation is a totally separate question in moral philosophy from the consequentialism vs deontology debate. One can be a consequentialist and yet endorse non-standard, non-additive theories of aggregation.
Here’s the structure of the rest of the article:
Clarifying the View
Objection #1: All Headaches Must Count the Same!
Objection #2: The Problem of “Much Worse Than”
1. Getting Clear
To state the view more precisely, I will help myself to the following notation. Let x, y, z, … designate different kinds of burdens (e.g., x = a mild headache, y = a week of intense pain, etc.). When a particular kind of burden, k, has multiple tokens, we denote the different token burdens as follows: k1, k2, …, kn. Next, let v(ϕ1, ϕ2, …, ϕn) designate a value function which takes in any number n of burdens, and outputs some real number representing the overall disvalue of that class of burdens.
So, if one is attempting to calculate the total disvalue of 3 mild headaches, we represent this as: v(x1, x2, x3). Using this notation, we can now express various aggregation views. For instance:
Standard Additive Aggregation
v(x1, …, xn, y1, …, ym, …) = n * v(x1) + m * v(y1) + …
To express the view that a class of burdens has a bound, we will need to help ourselves to one further piece of notation: let rϕ designate a real number between 0 and 1 (inclusive), representing the common ratio for some kind of burden ϕ. We can express one version of bounded aggregation as follows (I will call it Simple Bounded Aggregation [SBA] because I actually think there are some changes to be made to the view, but that won’t be the subject of this post):
SBA claims that, for each kind of burden ϕ, the total disvalue of n-many ϕ’s can be calculated as a geometric series. Thus, the total disvalue of a class of different kinds of burdens will be each individual geometric series for each kind in the class, summed together.
Okay, now lets consider some objections.
2. All headaches count the same!
Probably the first objection one will want to raise is that SBA treats headaches as though they have different disvalues, which is totally implausible. Each headache is equally disvaluable! A second headache is worth -1, just as much as the first one is. So, SBA must be false.
There are actually two, subtly different, ways of making this objection.
The first way of making this objection is to object to the fact that bounded aggregation entails that the amount of disvalue a headache contributes to a world is sensitive to external facts (namely, how many other headaches exist in the world). In particular, the worry is this: a common ratio (less than 1) entails that, as a kind of burden k is iterated in an outcome O, each subsequent token of k contributes less to the overall disvalue of O. But how can this be plausible? This would mean that the individual disvalue contributed by a token burden is determined by what else exists external to the token burden.
First, it is important to note that SBA does not entail that any token burden is any less bad for the person experiencing the burden (so-called subjective disvalue). For instance, every additional person in H who experiences a mild headache does not thereby experience a headache that is any less painful. The question, rather, is how much total (objective) disvalue we should tack on to H given that this additional pain––in all its hedonic displeasure––obtains.
And it is here that, by my lights, the context-sensitivity of SBA is not problematic. After all, it would be implausible to insist that all of our moral ideals are determined solely intrinsically. Indeed, a great deal of them have the similar sort of context-sensitivity that is baked into SBA. Suppose, for instance, that one takes equality to be a moral ideal relevant to the goodness of outcomes. Now imagine we are in a world where Joe is at a total welfare of 80 and Sally is at a total welfare of 60. Suppose we are considering adding 20 units of welfare to someone’s life. It might be that adding 20 to Sally might do more good than adding 20 to Joe, at least from the perspective of equality. But notice that this is so even though, whether we add 20 units of welfare to Joe or to Sally, it is the exact same addition of welfare in either case. Thus, from the perspective of equality, the extent to which an addition of welfare improves an outcome is sensitive to facts external to the welfare itself. I struggle to see the absurdity in our value judgements being context-sensitive in this way. This feature seems to pervade many other ideals as well––maximin, prioritarianism, and even impersonal ideals like, e.g., rare art, appear to admit of context-sensitivity. Why, then, exclude bounded aggregation from the party?
The second way of making this objection is to claim that the problem is with the difference between identical token burdens. Take, for example, a stipulated geometric series for the disvalue of mild headaches: 10 + 5 + 2.5 + …. If Alice’s toothache was the first headache we considered (v(h1)), and Bob’s is the second (v(h2)), we might wonder: why is Alice’s headache receiving special privilege over Bob’s? Namely, why is it that Alice’s headache has a disvalue of 10, but Bob’s headache has a disvalue of 5?
This, however, is too quick. Note that SBA does not make any commitment about the individual disvalue of any particular headache. What SBA says is that any collection of burdens has a total disvalue that can be calculated vis-à-vis a geometric series. So, given that a headache has a disvalue of 10 and that we stipulate the common ratio to be ½, what SBA tells us is that v(h1, h2) = 10 + 5. In other words, the view only entails that an outcome with Alice and Bob experiencing headaches has a total disvalue of 15. It does not say anything about how much disvalue Alice or Bob’s headaches individually have in that outcome. Now, of course, we have that v(h1) = 10. But all this means is that, in a world where the only burden that exists is Alice’s headache, the total disvalue in that world is 10. But this is perfectly consistent with v(h2) being equivalent to 10 as well––for that just means that in a world where the only burden is Bob’s headache, the total disvalue is 10.
To put things another way, SBA is a view quantifying over collections of burdens. It says nothing about how much disvalue each individual burden within that collection is contributing. It is not problematic for the bounded aggregationist to hold that v(h1) = 10, v(h2) = 10, and that v(h1, h2) = 15––to assert otherwise would be to assume an additive picture.
3. The “Much Worse Than” Objection
Another objection that might be levied against bounded aggregation has to do with some unintuitive normative judgements that all bounded views of aggregation seem to produce––in particular, about the “much worse than” relation.
Imagine an outcome A with a single person who is tortured for a year. Now imagine that a malicious individual transforms outcome A into outcome B, where 999 more people are tortured for a year (making a total of 1000). Now imagine further that outcome B is transformed into outcome C, where 999 more people are tortured for a year (totaling 1999). Clearly, C is worse than B, and B is worse than A. Additionally, B is much worse than A, just as C is much worse than B. However, it seems that bounded views cannot render this last judgement––that C is much worse than B. For, according to bounded views, the amount of disvalue contributed by a kind of burden decreases exponentially as we iterate. So, in the case of torture, it is a direct commitment of bounded aggregation that the difference between the disvalues of A and B is much larger than the difference between the disvalues of B and C (indeed, the difference is several orders of magnitude!), and so it seems that, while C is certainly worse than B, bounded aggregation commits us to judging that C is only a “little worse” than B. And this point generalizes in a rather worrisome fashion: if we consider further outcomes D, E, F, … where, each time, an additional 999 people are tortured for a year, eventually, going from, e.g., outcome Y to outcome Z, while worse, adds almost no disvalue at all. But, certainly, if anything is absurd, it is the claim that Z is “barely worse than” Y.
This is pretty bad. If bounded aggregation really entails that Z is “barely worse than” Y, it would be a non-starter: at least for me.
As such, I will offer one possible response to this troubling objection. First, it is important to see that this objection relies on the following account of “much worse than”:
Absolute Difference: The extent to which an outcome, O1, is worse than another outcome, O2, is determined by the difference between the total disvalues of O1 and O2.
The Absolute Difference account of “much worse than” entails that, if the difference between the total disvalues of C and B is some small number s, and the difference between B and A is some large number l, then B is much worse than A, but C is only slightly worse than B. And, indeed, we implicitly relied on this account when explicating the objection––for we argued that bounded aggregation entails that C is only slightly higher in absolute disvalue than B, which, naturally enough, is supposed to entail that C is only slightly worse than B.
The bounded aggregationist, however, should reject the Absolute Difference account. To see why, let us begin by noting that, in general, given a scale of measurement S for some quantity Q, the fact that S assigns some x value n and some y value m does not entail that the extent to which x is more Q than y is n – m (assuming n > m).
An example will be helpful: let us suppose that how rich one is is a function of how much money one has. Money, then, is a measure of richness––the more money one has, the richer one is. So, if Alice has 100,000 dollars, and Ben has 1,000 dollars, Alice is richer than Ben. And if Cecil has 1.1 billion dollars, and Dana has 1 billion dollars, then Cecil is richer than Dana. This much is determined by our commitment to money as a measure of richness. But now suppose that we are interested in knowing how much richer Alice is than Ben. In particular, suppose we are interested in knowing whether the extent to which Alice is richer than Ben is equivalent to the extent to which Cecil is richer than Dana. Some might argue that Cecil is much richer compared to Dana than Alice is to Ben, since the difference in money between Cecil and Dana is larger: Cecil has 100 million more dollars than Dana, whilst Alice has only 99,000 more dollars than Ben. Others, however, might argue that the opposite is true: Alice is much richer compared to Ben than Cecil is to Dana. And they might instead appeal to comparative ratios: Alice has 100 times the money Ben has, whilst Cecil has only 1.1 times the money Dana has. My purpose, of course, is not to settle this debate. Rather, my point is that there is debate to be had. That money is a scale of measurement for richness does not settle what the appropriate attitudes are about how much richer x is than y. We might put things like this: even if money is a measure of richness, no “cardinal” judgements follow about how much richer an x with money n is than a y with money m. All that follows is an “ordinal” judgement, namely, that x is richer than y, since n > m.
One reason that scales of measurement, in and of themselves, only determine ordinal, and not cardinal, judgements is that a scale of measurement for some quantity Q can have Q distributed across the scale in various ways. For instance, suppose we’re interested in measuring the difficulty of running a race. Let’s further assume that distance can be a measure of difficulty of running a race (assume, for instance, that the races whose difficulty we shall be measuring are equal in all other relevant factors, e.g., slope, terrain, climate). So, the longer a race is, the more difficult it is. We might, however, think that the following is true: not only does each additional mile in a race make the race more difficult, but it makes it exponentially more difficult. Each additional mile is even more difficult than the last. So, increasing a race from 2 miles to 3 miles results in an increase in difficulty of d, but increasing a race from 3 miles to 4 miles results in an increase in difficulty of k × d. If true, this would mean that, while distance is a measure of race difficulty, distance is not a scale on which race difficulty is evenly distributed. Instead, units of difficulty become more densely packed as we move along the scale, such that each unit increase of distance results in more and more of an increase in difficulty. Indeed, such uneven scales of measurement are rather common. Many scales of measurement in the natural sciences are logarithmic: e.g., the Richter scale, which measures the magnitude of an earthquake, is such that the difference in ground motion between a 1.0-rated and 2.0-rated earthquake is roughly 90 microns, whilst the difference between an 8.0-rated and 9.0-rated earthquake is roughly 900 million microns in ground motion. Thus, we may well be inclined to say that the difference between a 9.0 and 8.0 earthquake is much larger than the difference between a 2.0 and 1.0 earthquake. If so, this is because, whilst the Richter scale is a measure of earthquake magnitude, qua logarithmic scale it is a scale on which magnitude is distributed unevenly.
I introduce this discussion to make the following point: the bounded aggregationist needn’t accept that how much worse x is than y is determined by the absolute difference between x and y’s disvalue. Value and disvalue are measures of, inter alia, choiceworthiness, goodness, badness, and various other value facts. But why think that, e.g., badness is distributed evenly across the scale of disvalue? Analogously to the Richter scale, the value scale may well be such that while an outcome A of disvalue 4 is worse than an outcome B of disvalue 3, and that an outcome C of disvalue 9 is worse than an outcome D of disvalue 8, it is nevertheless true that C is much worse than D, whilst A is only slightly worse than B. And, of course, the converse could equally be true, if, e.g., comparative ratios end up being the right way to determine cardinal judgements about worseness and betterness. The value function commits one only to ordinal judgements about which outcomes are better than which––it does not settle any cardinal judgements about how much better or worse any two outcomes are.
Of course, the bounded aggregationist will still have to spell out what their cardinal theory looks like: they will have to actually tell us what the scale is like. And I believe there is a plausible account available — though that will have to be for another post!

Notice that a theory of the good has nothing to do with whether you are a consequentialist or a deontologist — you can (and should) still have a theory of what things are intrinsically valuable even if you are a deontologist. What makes consequentialism distinctive (compared to deontology) is that it says that the only thing you need, in order to know what you ought to do, is a theory of the good.
You can avoid these objections by positing that torture corresponds to some infinite surreal number, which would avoid some of these worries. I don’t have the space to discuss this cool proposal, but there are worries for that approach too. See, e.g., some of the theorems in this piece.


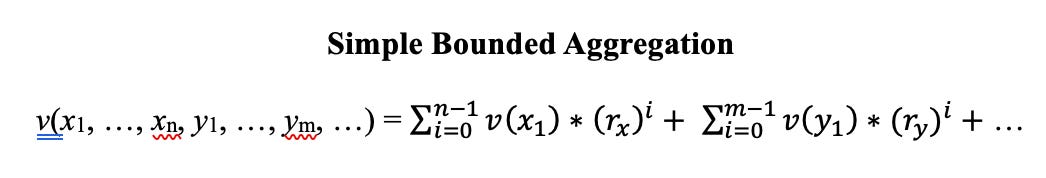
Very interesting post, and I certainly agree that this issue is (somewhat) separate from normative ethical issues! Though a few thoughts/objections:
1) I suppose I don't feel the pull of the initial intuition pump too strongly. Perhaps I'm just lost in the sauce, but the more I think about repugnant-style conclusions, the less I find them plausible, and something something scope-neglect.
However, denying the premises leading to these kinds of conclusions remains very counter-intuitive, even when I consider them more. This is more of a report than an argument though.
2) You say that the worry about external circumstances mattering isn't so bad once we realize its objective value rather than subjective value. I don't see this. Objective value matters in terms of what we ought to do, and it's still very absurd to me that what happens on distant parts of the universe can determine whether I should alleviate a headache or have some chance of stopping someone from getting tortured.
You give an example of egalitarianism. Maybe this is idiosyncratic, but I just think that that example shows that axiological egalitarianism is wrong! (Likewise for the other things you mention that have this issue.) Surely whether I should benefit John doesn't depend on welfare levels outside the observable universe or in the distant past!
Now things external to the situation you're considering can of course matter insofar as what you do might make some difference to what happens elsewhere or vice versa. The trouble is when completely seperate things that could never make any difference still have extreme importance for our decision-making. This just seems completely implausible for me!
3) Isn't your theory very sensitive to how we individuate kinds of harms? If we characterize headaches broadly, there might be very many, and the marginal headache is not very bad, however characterizing it in a fine-grained way, the marginal headache will be as bad as any other, since it will probably differ somewhat from other instances.
I have a hard time seeing any principled way of individuating kinds of harms other than as finely as possible, but doing so doesn't capture the intuitions you want, as we can run the torture vs. 1000 headaches counterexample with minutely differing headaches.
4) Small point, but it seems like if we live in a multiverse, infinite Universe or some similar theory, we get the result that nothing we do matters axiologically (or only thing we do regarding unbounded kinds of values matter axiologically) as the marginal value of our actions is 0 or infinitesimal. (This objection might be countered by your response to the "much worse than" objection.)
5) Finally, just a question: I wonder why you're a fanatic given this view? If value is bounded, it's surely not true that any small probability of value V can be outweighed by the magnitude of V?
That's a lot, and I suspect you have good things to say about all of them! Ultimately it's a matter of reflective equilibrium, and I just don't feel the initial pull away from unbounded value strongly enough to justify what I see to be extremely heavy costs.
Thanks for the great post! I have a couple comments:
1. I do think a logarithmic scale is maybe the right way to go. For example, if we intuitively feel a headache is a 2, and torture is 1000, then the "true" values are 10^2 and 10^1000. True, we can get enough headaches to outweigh the torture, but it takes 10^998 which is basically infinity. Also, for money, earthquakes, sound loudness, city size, etc., how big each feels is the log of the absolute size, so moral utility would just be another in a long list of examples of how human intuition works on a log scale.
2. Still, I love the idea of trying to get bounded aggregation to work mathematically. Here is my idea: write both numbers in base 2, adding leading zeros so they have the same number of digits to the left of the decimal. Then, use the digits of the smaller number to replace the zeros in the digits of the larger number. So for some examples, (1 + 1 = 1.1) (1.1 + 1 = 1.11) (100.1 + 010.1 = 101.101). This has the property that no amount of adding numbers less than 8 (or any other power of two) will ever get to 8. It's commutative by fiat (you have to start with the larger number), but I believe it is associative naturally (I don't have a proof but it worked in one example!)